How to Calculate Cut and Fill for Earthworks Projects
CROSS-SECTION METHOD
The cross section method involves plotting cross sections of the existing and proposed levels at regular intervals across the project site. For each of the cross sections, the cut area and the fill area is determined. The volume between each pair of sections is estimated by multiplying the average cut or fill area of the two sections by the distance between them. Once these volumes have been calculated for each pair of sections the total cut and fill volumes are obtained by adding them all together.
There are several different methods used to determine the areas of cut and fill, once the sections have been plotted. Perhaps the simplest (but most time consuming) method is to plot the sections on gridded paper and count the grid cells of the cut and fill areas. Multiplying the cell count by the area represented by each of the grid cells gives the cut or fill area for the section. Other methods include drawing the sections in CAD and exporting areas or calculating areas mathematically using the trapezoidal rule. The spreadsheet included with this article includes formulae which have automated the process of calculating section areas using the trapezoidal rule. This can save a great deal of time if you are using the cross section method.
The accuracy of the cross section method depends to a large degree on the distance you choose to set between the sections. Closer sections improve the accuracy of the estimate, but take longer to estimate. A balance has to be made between accuracy on the one hand, and speed of generating the estimate on the other.
One of the great advantages of this method is that cross sections are generated in the process. These provide a useful visual summary of the estimation, which present the cut and fill depths across the project in a very clear way. One of the disadvantages off the method is that it can be extremely laborious to extract cross sections from the drawing, and to determine the areas of the sections.
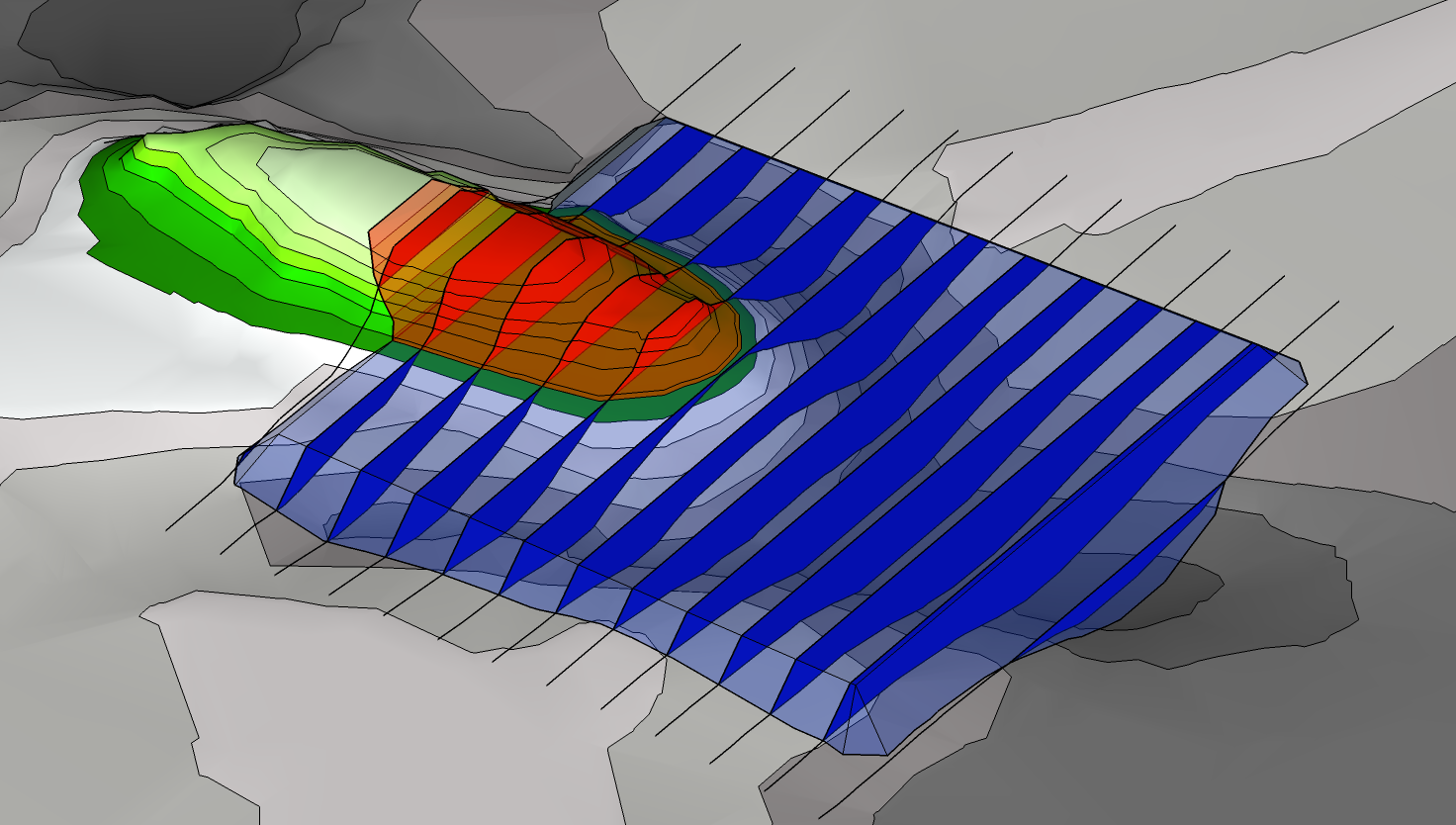
Sections are drawn at equal intervals through the project. For each section line the cut area and the fill area is determined. The volume between two sections is determined as the average area of the two sections multiplied by the distance between them. By adding together the volumes between all of the sections the total cut and fill volumes are obtained.
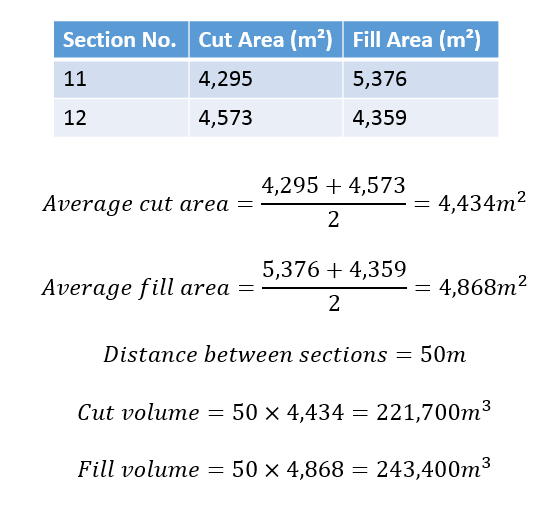
An example calculation for the volumes between two sections of the example shown opposite. This calculation is repeated for all of the sections, and the values are added together to get the total cut and fill volumes.
GRID METHOD
The grid method involves drawing a uniform grid onto a plan of the earthworks project, and taking off the existing and proposed ground levels at each node of the grid. With these values the average depth of cut or fill required on each cell of the grid is calculated, and the volume for each cell is obtained by multiplying the depth by the cell area. By adding the volumes for each cell together the total cut and fill volumes for the project can be estimated.
The cut or fill depth for each cell is found by subtracting the average existing level of the cell from the average proposed level. If the resultant depth is positive then this is a fill cell, while a negative value indicates a cut cell. In either case, the volume is calculated by multiplying the cut or fill depth by the area of the grid cell.
Once the volume has been calculated for each grid cell, all of the cut cells are added together to obtain the total cut volume. The same is done for the fill cells to get the total fill volume.
As with the cross-section method, the accuracy of the grid method depends upon the size of grid cell which is used. A compromise has to be made between the accuracy which is required, and the time which will be taken to produce the estimate.
An advantage of the grid method are that the basis of the estimate can be fully summarised on the site drawings, which presents a very clear summary of the calculations for others to check. One of the disadvantages are no graphical summary is generated for the estimation. Also, like the section method, the grid method is time-consuming and tedious to implement.
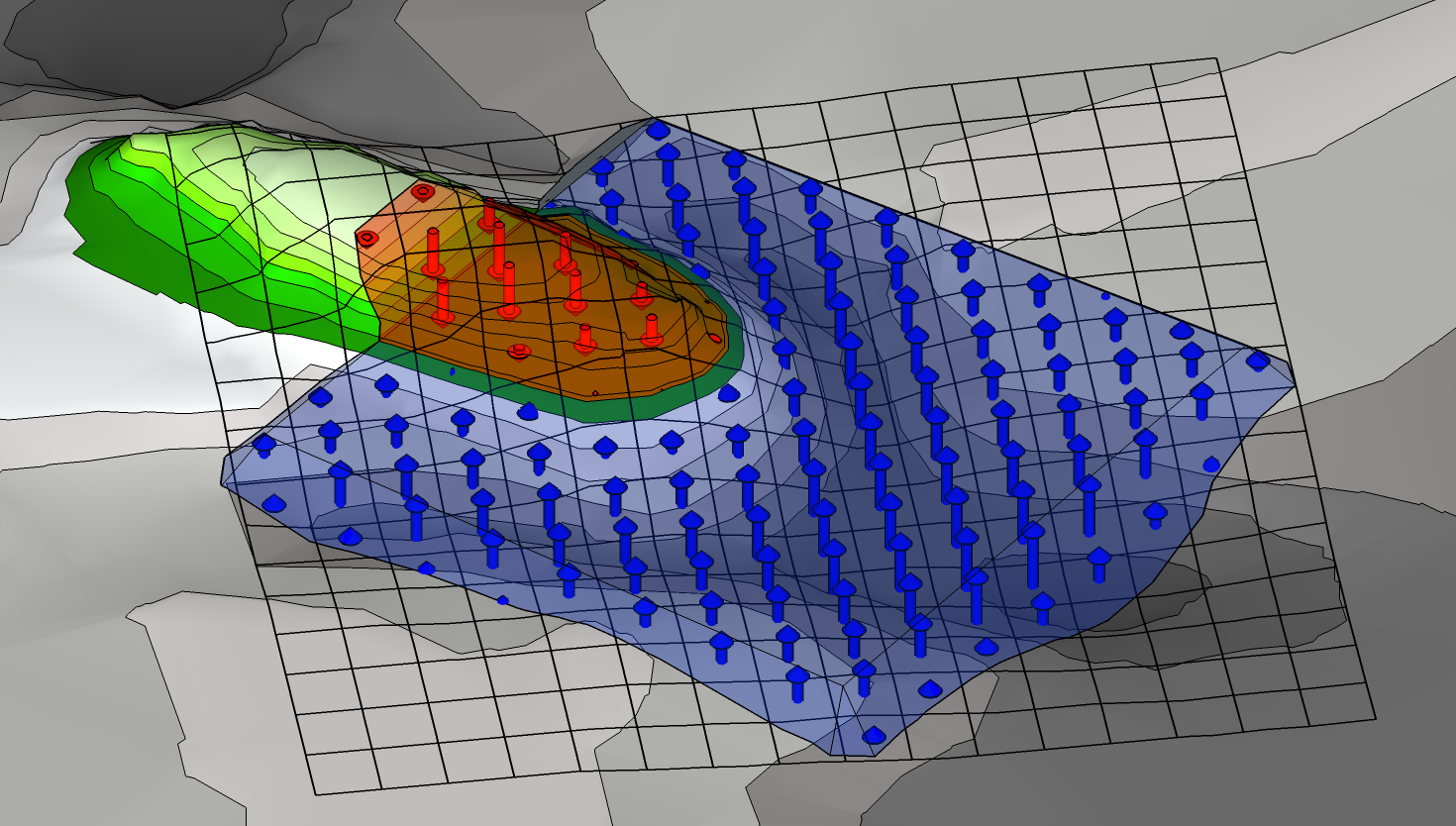
The average cut or fill depths are determined for each cell in the grid. From these depths the volumes of each grid cell can be calculated, and by adding the cell volumes together the total cut and fill volumes are obtained
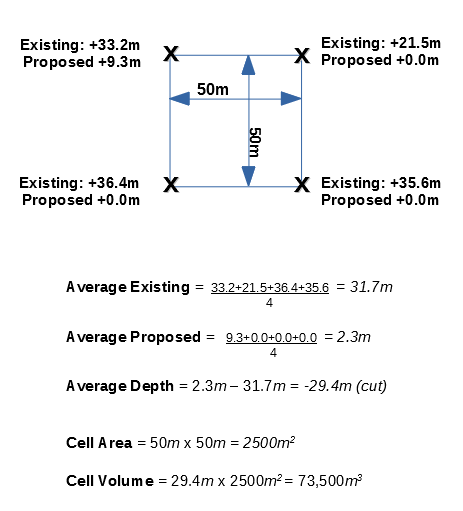
An example calculation of the volume for one of the grid cells, in the example above.
TRIANGULAR PRISMS
The third method that is commonly used to calculate earthworks volumes is the triangular prisms method. This is by far the most technically difficult method, but is also the most accurate.
This method starts by triangulating the existing terrain. This involves joining the points in the terrain to create a continuous surface of connected triangles. This is known as a Triangulated Irregular Network, or TIN for short. This step is repeated for the proposed terrain.
The next stage is to merge these two triangulations, to create a third triangulation which contains all the edges of the original triangulations. This will be used to perform the calculations, and merging the two input triangulations means that every detail of both the existing and the proposed will be included in the calculations. This is the basis of this method’s accuracy.
The last stage is to calculate the cut and fill of each vertex on the calculation TIN. These values can be used to calculate the cut and fill for each triangle, and the total volumes are easily obtained by adding all the triangles together.
Due to the great complexity of these calculations and the thousands of triangles that are generated it is not practical to calculate triangular prisms by hand. Instead, these calculations are done with specialised software like Kubla Cubed. However, it should be noted that not all earthworks software uses this method; some software calculations are based on automated high-density grid calculations or the cross section method used in conjunction with TINS.
There are several great advantages to the triangular prism method. First and foremost, this method is the most mathematically complete of the three. Since every detail of the existing and proposed terrain is retained in the merged triangulation nothing is lost in these calculations whereas all other methods accept a certain degree of loss due to details falling within the density of the grids or cross sections.
Another advantage of this method is that you can represent the finest level of detail, even if a site is very large. Using both the grid and cross section methods you have to define the density of the grid squares or sections, and any detail that is within this spacing is liable to be lost. With the triangular prism method, on the other hand the finest level of detail can the represented even in very large sites, as having a high density of triangles in one area does not have the knock on effect of requiring other areas of the site to have the same detail. This means that even on a very large site you can represent a small trench without any loss of accuracy.
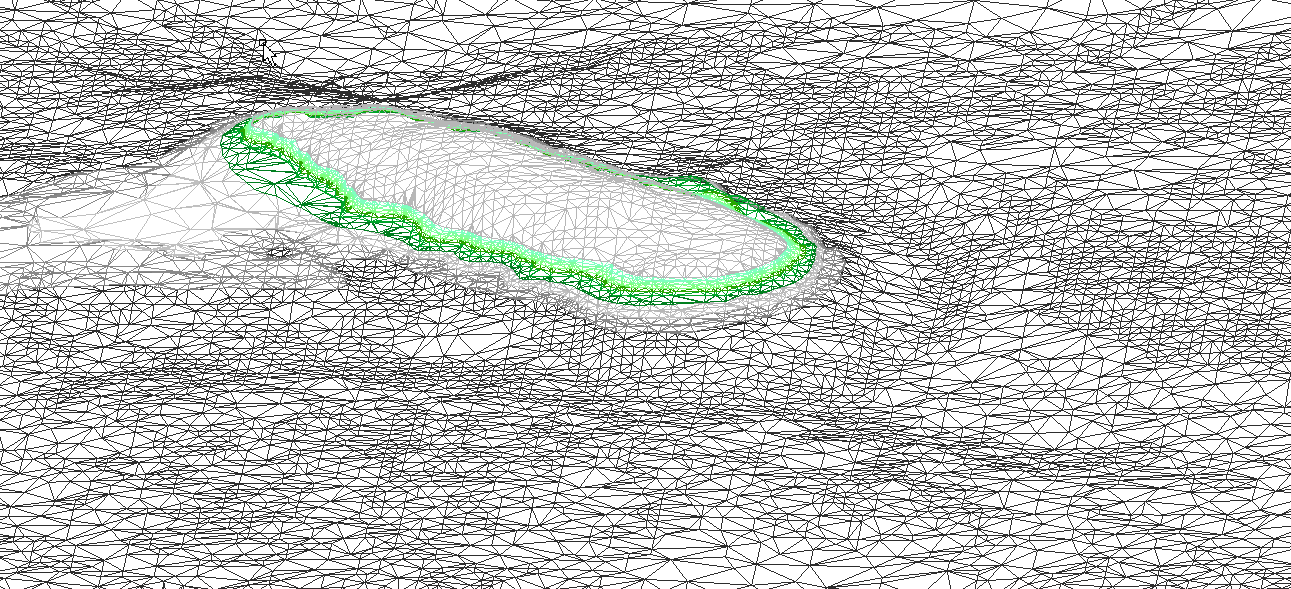
Triangulation of existing terrain. Note the smaller triangles in areas where more detail is required. The proposed surface is triangulated in the same way.
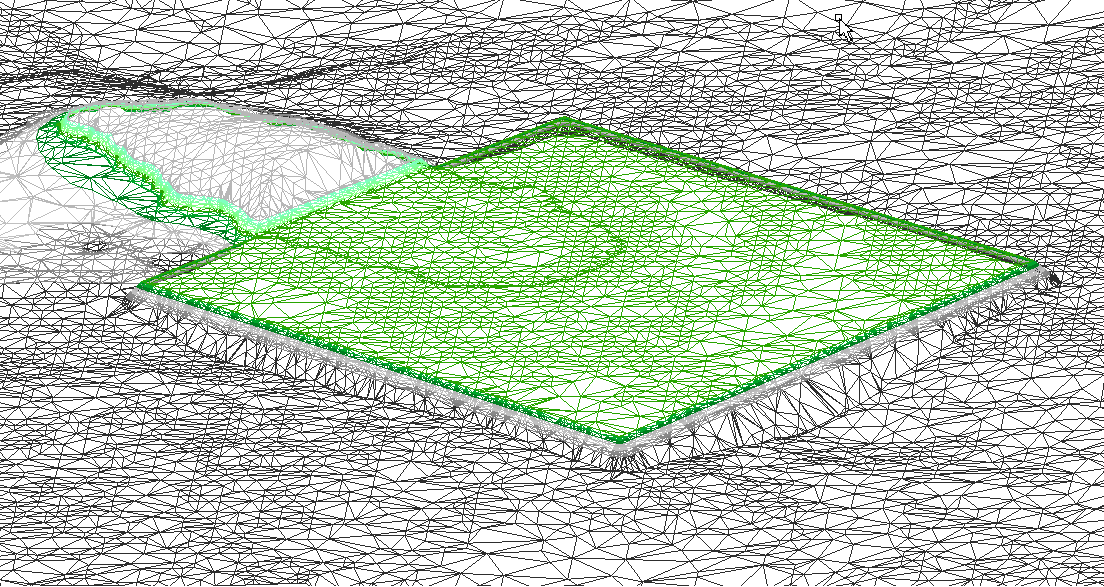
Merged triangulation, which contains all the edges of the existing and proposed triangulations. The fact is key to the accuracy of this method, as all the features of both surfaces will be represented in the calculations
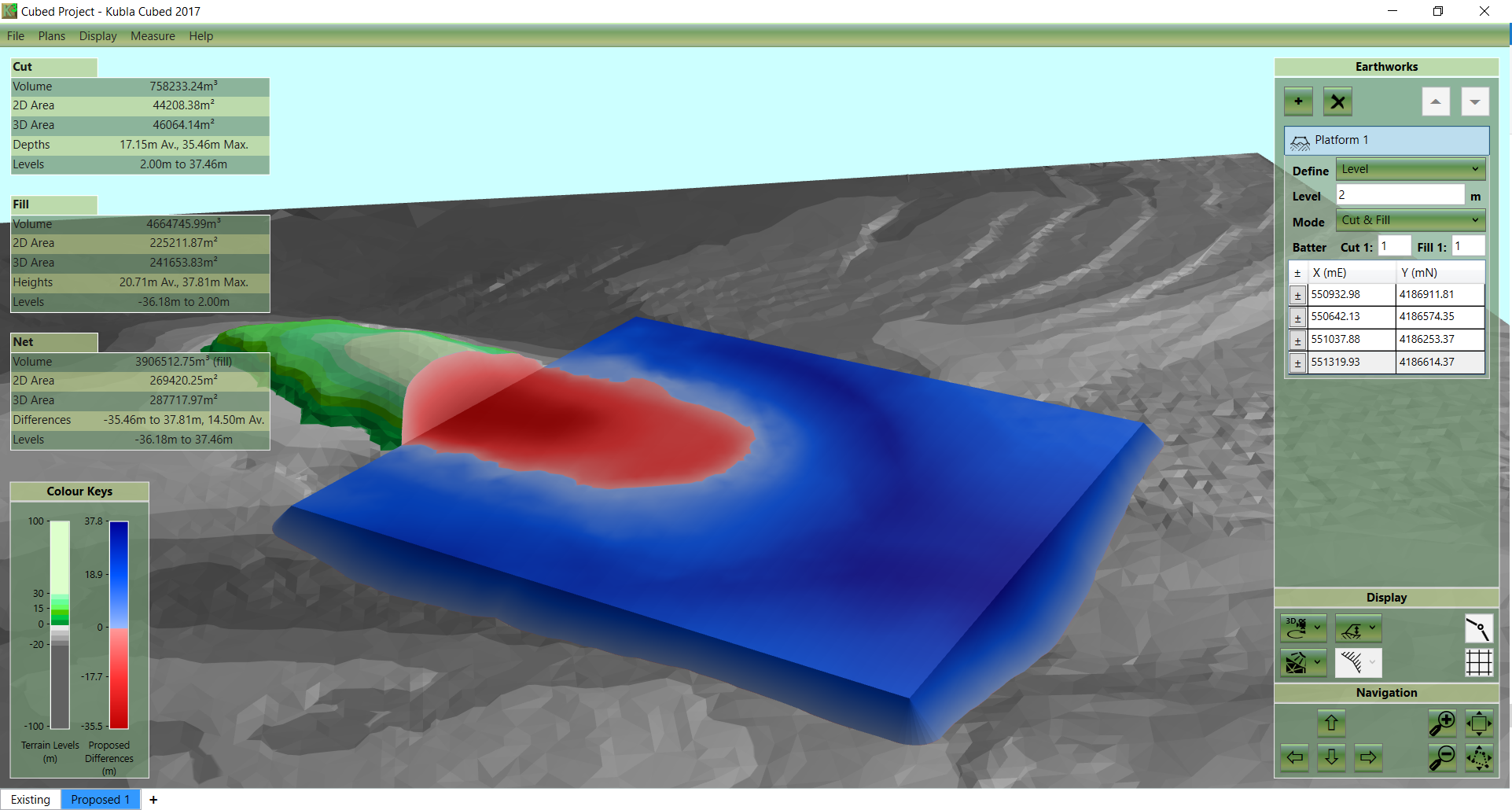
A secondary benefit of any software-based solution is the speed of input and the ability to view 3d images to validate results.
FURTHER RESOURCES
- There is a video which covers the same content as this post here.
- Download the free Kubla Cubed Lite to complete the calculations mentioned above.
- Buy a Kubla Cubed Professional licence.
- There is a wikipedia page which compares the different software for earthworks estimates here.

0 Comments
Trackbacks/Pingbacks